E=4.44Φf[V]
この式なんか見たことある・・・。
電験の機械科目を勉強していくと誘導機あたりの話でこの式が突如として出現する。電験用のテキストを見ると当たり前のように誘導起電力はこの式ですと平然に記載してくる。
はっきりいって暗記してもすぐ忘れる。
そもそも誘導起電力って
フレミングの右手の法則でいう中指のはなし。
誘導電動機の場合、回転磁界によって回転子が相対的に動いたように見えて、磁界の方向・運動の向きが決定されて誘導起電力(誘導電流)が発生する。
これが誘導起電力であり、計算式として4.44という不可解な数字は次のような過程で導きがされている。
一次巻線の場合(固定子)

一次巻線といえば・・・固定子である。
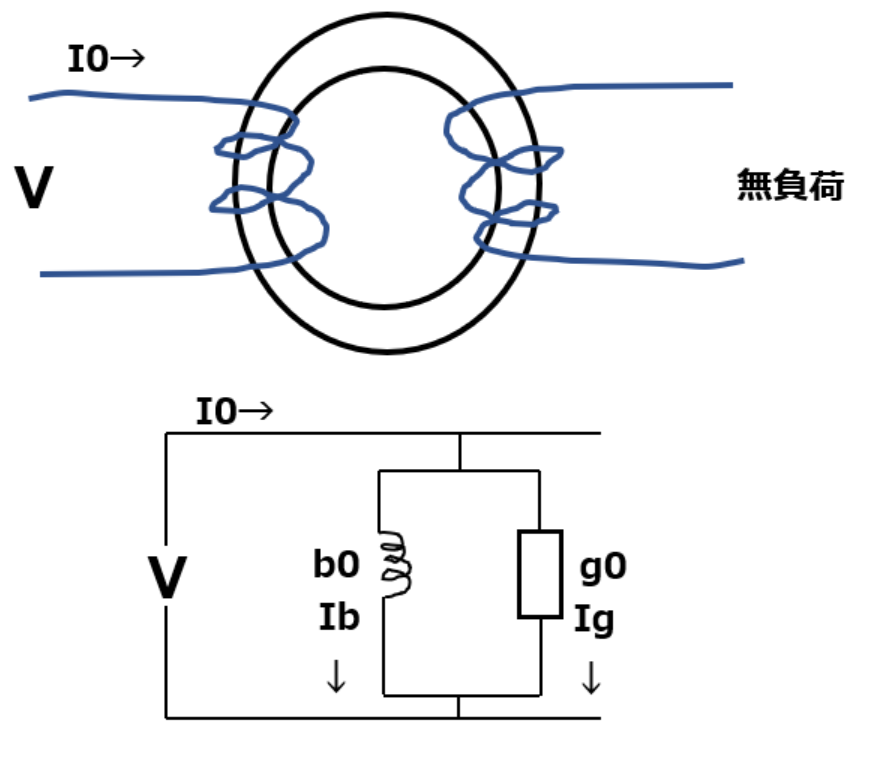
誘導電動機の二次側を開放したとする。かご形誘導機の場合は二次側が回転子になるので、回転子鉄心のスロットに収まっている導体バーが対象となる。通常は端絡環で短絡(通電)されているが、仮にこれを開放した場合を考える。
この状態で固定子に電源を供給してみる。
固定子には回転磁界が発生する。
ただし二次側は開放している為誘導電流は流れないし、回転もしない。
ここでこんな式が登場する。
sin2πft
正弦波交流電源は直流電源と違って時間とともに変化する。固定子に供給される電源も交流なので一緒。
たとえば100Vの交流電源であれば
最大値:100×√2=141V
実効値:100V
と習っているから、 正弦波中のある一点の値を知りたい時(瞬時値)
e=Emsin(2πft)と表せる。
Vmは電圧の最大値。正弦波中の振幅(高いところ)になる。
2πfは角周波数ωと呼ばれrad/sで表される。
角周波数はめっちゃ大切で電験の理論・機械でも良く出てくる。fは周波数だから50Hzの場合、1秒間に50回の振動(周期)がある。2πは360度・・・ということは円一周になる。
つまり50Hzの周波数の場合、1周(360度・2π)するには1周期だから0.02秒(1/50)。50周するにはちょうど1秒かかる。
2πfは1秒間に何回転しているかが分かる式となる。
これを角周波数(rad/s)と呼ぶ。
忘れそうになったら単位を見てほしい。1秒間に何ラジアン進むかと分かるから。

sinは正弦関数とも呼ばれ半径1の円とサインカーブが対応する。
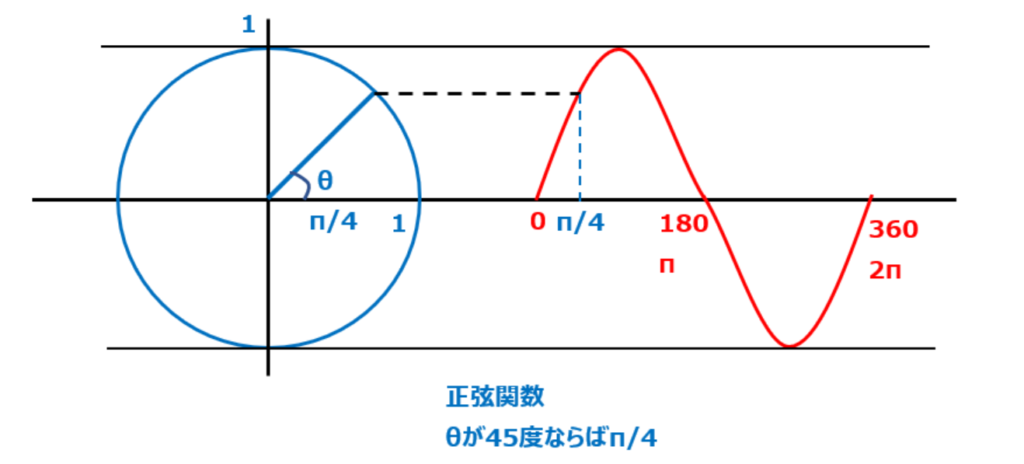
ここで
v=Vmsin2πftの式に話を戻すと
e=Emsin2πft
e=Emsinωt(ω=2πf)
e=Emsinθ(θ=ωt)
となり、これが瞬時値となる。
回転磁界によって回転子に起電力を誘導する
Em=2πfΦ
e=(2/√2)πfΦ (実効値に変換の為√2で割る)
e=√2πfΦ
e=4.44fΦ (コイル一巻きあたりの起電力)
(編集中です)


コメント