誘導電動機のトルクは一次電圧の2乗に比例する。(電源電圧の2乗に比例する)
トルクT∝Vの2乗
同期角速度と同期ワット
同期速度においてトルクを出したと仮定した場合のトルクを同期ワットと呼ぶ。
トルクはN・mで表されるが、同期ワットは同期速度での値なので同期ワットをP同期とすると
P同期=T×ω同期 (ω同期は同期角速度とする)
ω同期(同期角速度)=2πf=2π(Ns÷60)
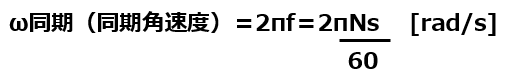
ωは角速度なので2πfになる。(秒間に円を何周したのか、何radか)
fは周波数なのでNs÷60にも置き換わる。

よって同期角速度ω=2π(Ns÷60)が求まる。
P同期=T×ω同期
すなわち同期ワットは同期速度時のトルクということになる。
P同期をPs、ω同期をωsとすると
Ps=T×ωsとなる。
難しく考えないで定格回転数時のトルクに同期角速度を掛け合わせたものが同期ワットになる。
この同期ワットの考え方として、同期速度となるとすべり=0と考えてしまう傾向にあるが(自分もそう)、あくまであるすべり中の同期速度を考えてあげる。
このある回転中の同期速度と回転速度を同期速度に見立ててやるのが同期ワット(トルク)になる。
同期速度Nsを一定にすると同期ワットはトルクに比例する。
ちなみにこのPs(同期ワット)は後々出てくる二次入力(P2)とイコールになる。
誘導電動機の機械的出力
誘導電動機のトルクは固定子に供給された電源が二次側に相当する回転子に誘導されて回転子の回転によって機械的に出力される。この過程において抵抗損や鉄損などに失われるが、機械的出力をP機械・回転角速度をω回転とすると
P機械=T×ω回転[W]となる。
機械的出力は回転角速度×トルクとなる。
P機械をP0・ω回転をωrとすると
P0=T×ωrとなる。
ちなみにωrは同期角速度ωsからすべり分遅れているので
ωr=ωs(1-s)とも表せる。(同期角速度からすべり分遅れているので例えばすべり5%ならば同期角速度ωs×95%が回転角速度ωrとなる)
よってP0=T×ωs(1-s)に変換も出来る。
軸出力
固定子に供給された電源は回転子に抵抗損や鉄損と失いながら機械的出力P0として出力され、ベアリングやブラシ等の抵抗によりさらに出力を失われ軸出力となる。
この軸出力が実際に取り出される最終的な出力でありPmと表すと
Pm=P0ー損失となる。
(つづく)
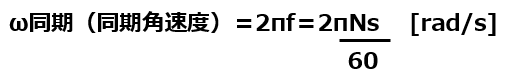



コメント