電験三種で使用する三角関数とラジアンの関係性と忘れない覚え方

電験三種を受験するにあたって避けて通れないのが三角関数。

それと併せてラジアンの関係が理論を初めとした計算問題に出題されており、ベクトルなどの問題も出る。

両者とも参考書やネットで調べれば理論的な事から細かく記載されているが、僕は内容を理解するのに苦労した。

暗記してしまっても良いがすぐに忘れてしまう為、自分なりの覚え方を記載するので参考になればと思う。

いきなり暗記だが最低限の事なので心配はしてない。

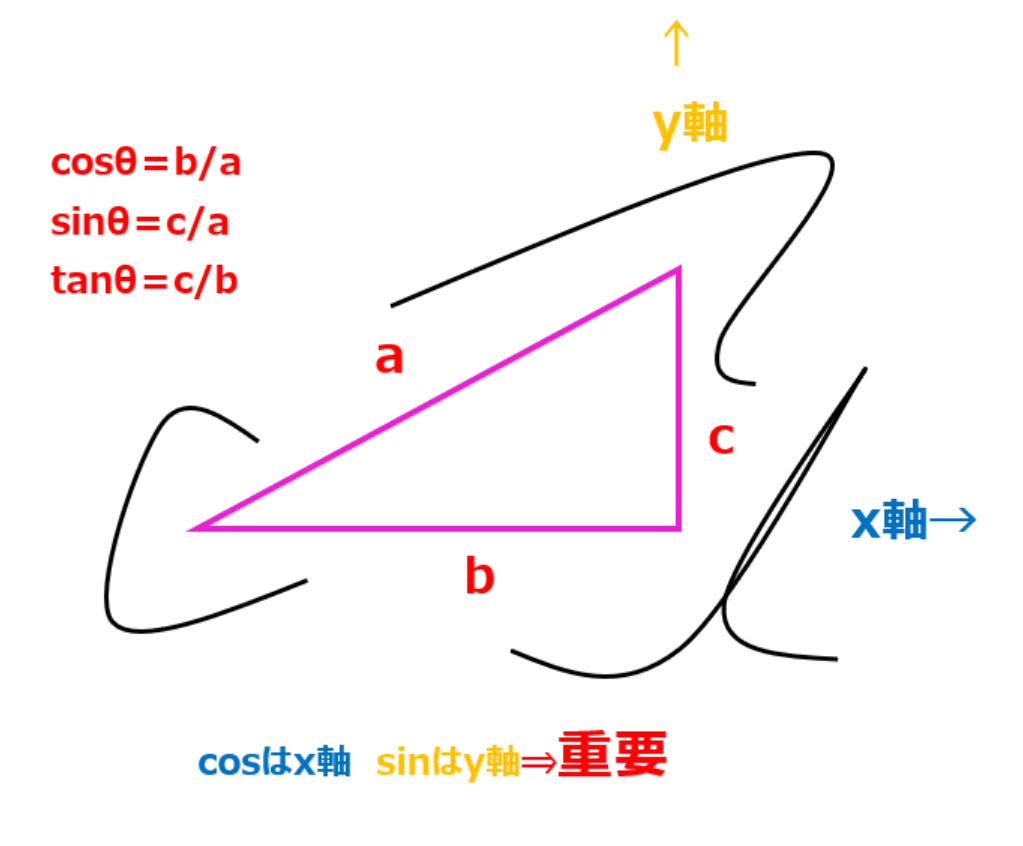
中学で習った三角関数。電験で役に立つとは思ってなかったよ。

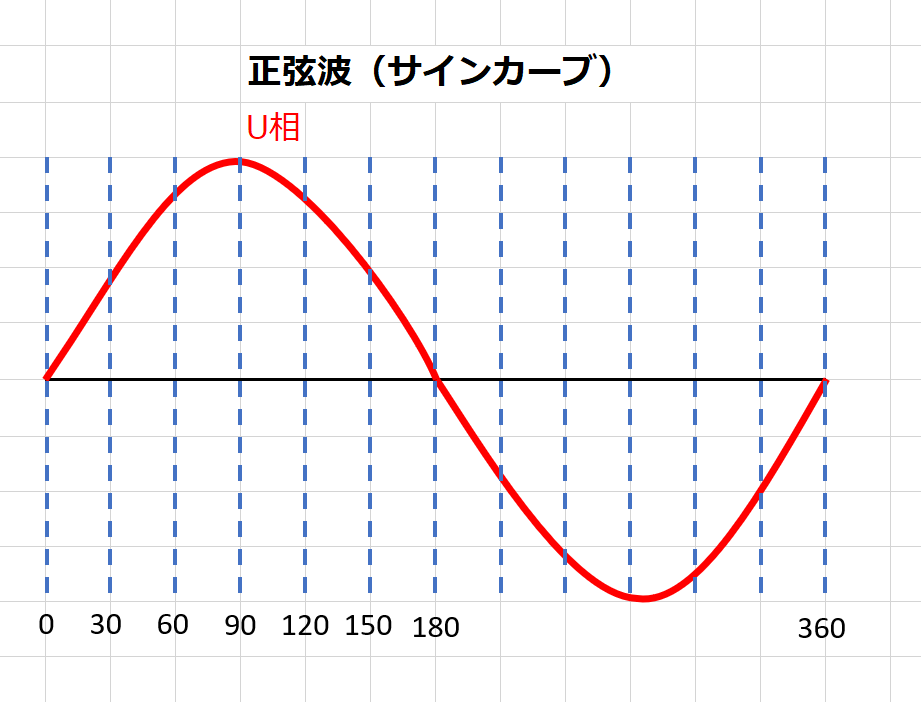
大切なのは、cosはx軸に対応・sinはy軸に対応という事。

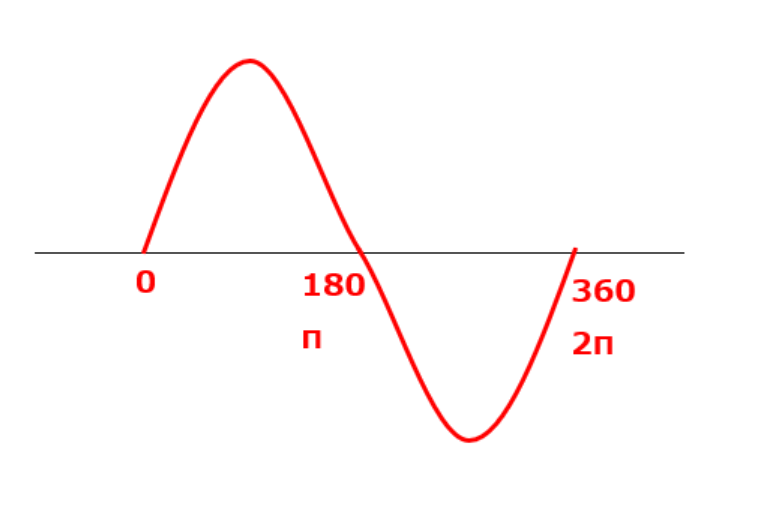
あと大切なのが1周期において0度から360度になる事。また、ラジアンが2πになる事。

360度＝2πがわかっていればあとは暗記しなくても大丈夫。

180度は360度の半分（1/2）なのでラジアンは2πの半分πになる。

じゃあ30度は何πになるのか。ここら辺から分からなくなる。

単純な考え方で良く、ラジアンと角度の換算表があるがあんなのは覚えなくても良い。90度であればπのさらに半分でπ/2になる。30度であれば90度の1/3なのだからπ/2×1/3＝π/6になる。かんたんだ。

そもそも電験の問題で出てくるのは、30度・45度・60度・90度（以降一緒）あたりになる。

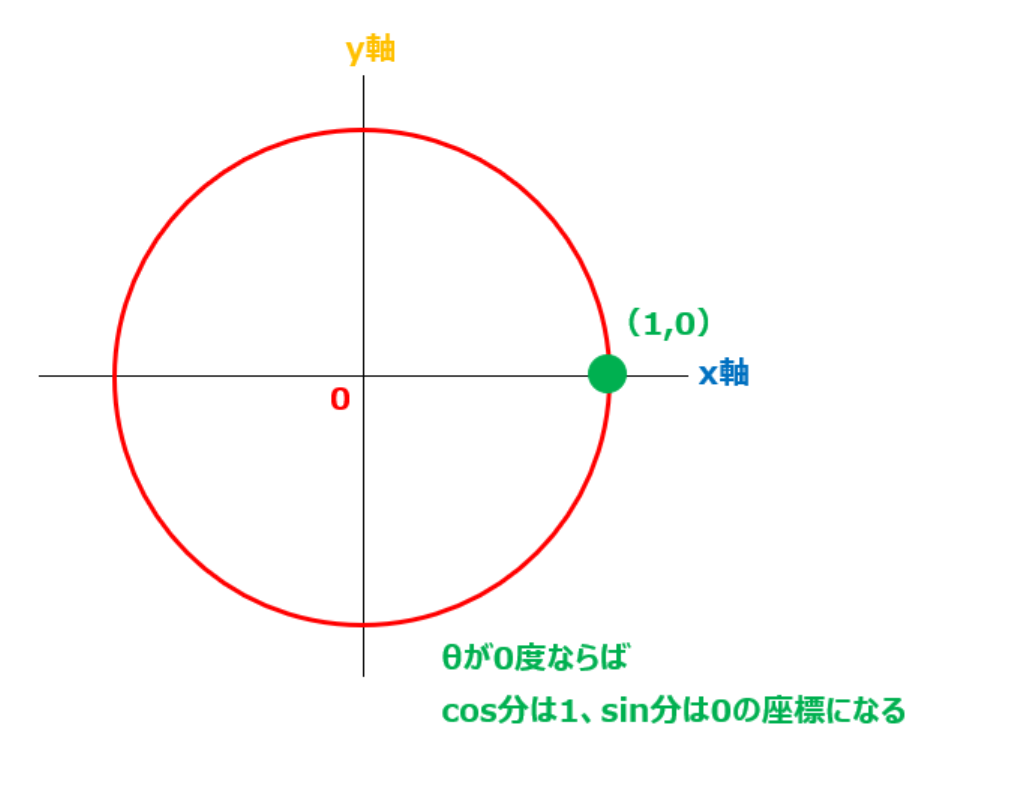
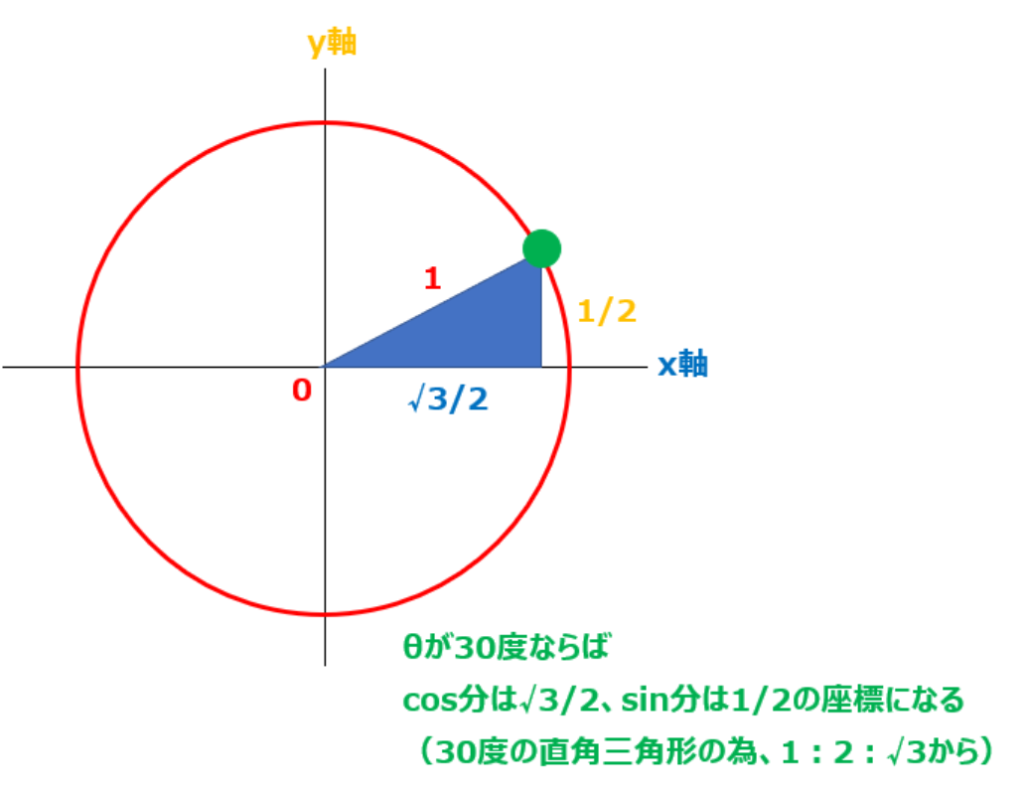
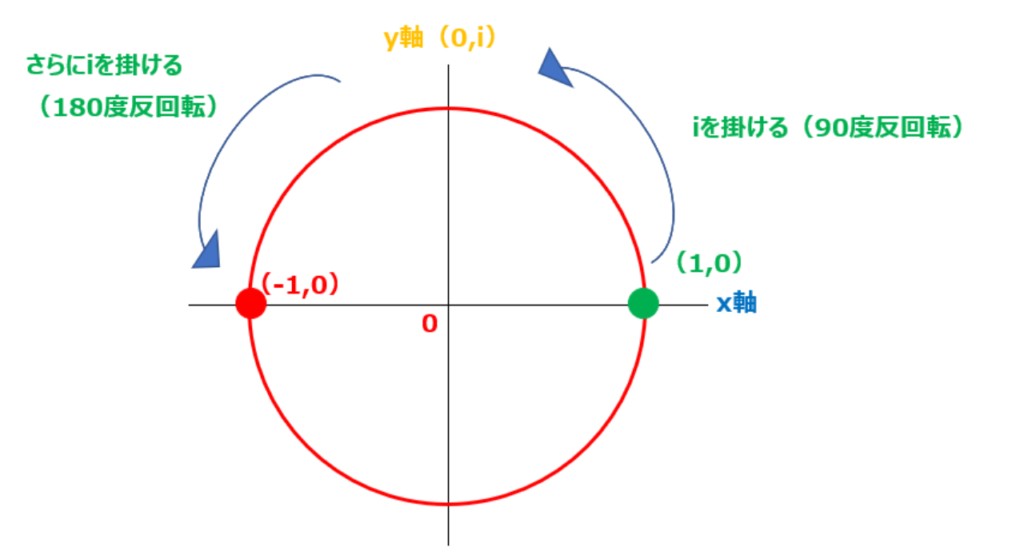
ちなみにy軸は虚数（i）である。これめっちゃ重要。

iにiを掛けると-1と良く出てくる。これを考えると

x軸（1,0の座標）に点があったとして、この点をy軸（0,1）に移動させる為には90度反時計回りさせなければならない。

ここで一つルールとして虚数iを点に掛けると反時計回りに90度回るという性質を覚えておく。（とりあえず暗記）

このルールに従って（1,0）の点を（0,1）もしくは（0,i）の位置に移動させるには90度反時計してやれば良いのでiを掛けて回転させてやる。

すると点は（0,1）もしくは（0,i）に移動するが、またiを掛け合わせると（-1,0）となる。

結局最初の点（1,0）からiを二回かけたので、-1となる。

この円周上での動きが電気計算にも絡み、特にインピーダンス（コイルやコンデンサ）に深く関わってくるので絶対に覚えなくてはならない内容。例えばコイル抵抗はiXLΩなどと考えられ電験合格には避けては通れない。

僕は工業高校卒なのでろくに数学をやってきては無いですが、理論的に覚えるよりもとりあえず絵に書いてイメージすることが大切と思う。実際に電験を受験した際も絵を多く書いた。

電験二種からはそうもいかないので数学を0からやっていかなくてはならないが、重い腰を上げるためにも理論的に考えずイメージして、次のステップアップとしてなぜそうなるのかを後で勉強した方が良い。